Hierarchisches Material - Operationen im Dezimalsystem

Zum hierarchischen Material gehören alle Materialien, die den Aufbau des Dezimalsystems mit den Farben Grün, Blau und Rot entsprechend der Stellenwerte 1, 10 und 100 darstellen, wie auch 1.000, 10.000 und 100.000 und 1.000000

Markenspiel

Punktspiel (im Untermenü Hierarchisches Material II)
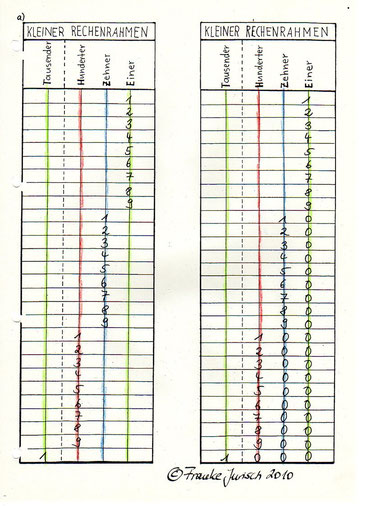
Kleiner Rechenrahmen
Hierarchie der Zahlen (im Untermenü Hierarchisches Material II)
Großer Rechenrahmen
Große Multiplikation (Schachbrett)
Liegender Rechenrahmen
Bankspiel (im Untermenü Hierarchisches Material II)
Große Division (Apotheke)

Markenspiel

Ziele:

Kenntnisse über das Stellenwertsystem (Dezimalsystem) festigen / Üben und Sichern der Addition, Subtraktion, Multiplikation und Division

Hinführung:

Ich lasse das Kind je einen 1er, 10er, 100er und 1000er vom Goldenen Perlenmateial holen. "Gib mir mal den 1er!" Ich lege ein grünes 1er Plättchen unter den goldenen 1er und sage: "Das ist genauso viel wert wie ein 1er. Das ist auch ein 1er!" So verfahre ich auch mit den anderen Stellenwerten. Mit der Drei-Stufen-Lektion führe ich nun die unterschiedlichen Stellenwerte der Marken ein.

Hier wird die Ablösung vom Goldenen Perlenmaterial vollzogen. Im Gegensatz zu den Perlen fehlt die konkrete Menge - neu ist auch, dass der Stellenwert als Zahl auf den Marken abgebildet ist. Zunächst wird mit den Kartensätzen gearbeitet, doch im Laufe der Arbeit werden diese durch Tischkartensätze sowie schließlich Papierstreifen ersetzt.

Es wird vorausgesetzt, dass die Mengen bekannt sind sowie das Tauschen in den nächstkleineren Stellenwert im Dezimalsystem.

Übungen:

- vorgegebene Zahlen mit den Marken darstellen und lesen / Marken legen und aufschreiben / lesen lassen

Addition (mit Übertrag)

Da das Kind das Wesen der Addition bereits kennt, lässt sich hier schon gut mit einer aufbauenden Aufgaben-Kartei arbeiten. Es kann gleich die Addition mit Übertrag erfolgen, da das Kind das Wechseln von den Goldenen Perlen her kennt.

Übungen:

- Aufgabenkartei mit rückseitiger Fehlerkontrolle.

Multiplikation mit einstelligem Multiplikator:

Die Multiplikation mit dem Markenspiel erfolgt additiv und ist somit genauso wie bei der Addition durchzuführen.

Einführung:

Auf drei Papierstreifen bzw. mit drei Tischkartensätzen wird die Aufgabe 2321 • 3 dargestellt, jeweils mit den entsprechenden Marken darunter. Ich schiebe die drei Zahlen nach rechts raus und fordere das Kind auf, die drei Zahlen vorzulesen. "Wie oft liegt die Zahl da?" -> drei Mal. "Gut, du kennst das schon." Ich nehme zwei Multiplikanden weg, lasse nur einen liegen und schreibe auf einen weiteren Papierstreifen • 3. Das Kind rechnet die Aufgabe und legt das Ergebnis mit dem Kartensatz.

Übungen:

- Aufgabenkartei mit rückseitiger Fehlerkontrolle.

Subtraktion (ohne Übertrag):

Bei der Subtraktion empfiehlt es sich, zunächst eine Aufgabe ohne Übertrag zu legen um vorerst nur Anordnung und Schritte als neue Schwierigkeit zu isolieren.

Ich schreibe zunächst den Minuend auf einen Zettel bzw. lege diesen mit dem größeren Kartensatz (da größte Zahl) an den linken oberen Teppichrand. Die Aufgabe lautet zum Beispiel: 3325 - 1124. Mit einem weiteren Zettel bzw. mit einem kleineren Kartensatz lege ich den Subtrahend deutlich rechst neben den Minuend. Ich bitte das Kind die entsprechenden Marken unter den Minuenden zu legen. "Von dieser Zahl wollen wir nun diese subtrahieren. Was heißt subtrahieren noch mal?" -> Wegnehmen! "Gut. Beginne bei den 1ern. Wie viele 1er sollen weggenommen werden?" -> Vier 1er. Ich schiebe vier 1er vom Minuend unter den Stellenwert der 1er des Subtrahenden. Das Kind beendet die Aufgabe.

"Das Ergebnis ist das was übrig bleibt!" Die unter dem Minuend verbliebenen Marken werden nun mit deutlichem Abstand als Differenz unter den Subtrahenden gelegt und mit einem weiteren kleinen Kartensatz dargestellt. Der große Kartensatz des Minuenden wird über den Subtrahenden geschoben.

Auch hier kann die Aufgabe in ein bereitliegendes Forumlar übertragen werden.

Übungen:

- Aufgabenkartei mit rückseitiger Fehlerkontrolle

Division:

Zunächst folgt eine Divisionsaufgabe mit einstelligem Divisor, ohne Umtäusche und ohne Rest. Hier am Beispiel der ersten Karte einer aufbauenden Kartei: 4844 : 4. Am linken Teppichrand legt das Kind den Dividenden mit Kartensatz und Plättchen aus. Der Divisor wird durch vier 1er-Kegel (grün) dargestellt. Beginnend bei den 1000ern werden die Märkchen nun gerecht verteilt. Das Ergebnis ist das, was einer bekommt.

Auch hier kann die Aufgabe wieder in ein entsprechendes Formular übertragen werden.

Mehrstelliger Divisor:

Die Aufgabe lautet zum Beispiel 264:12. Wieder legt das Kind den Dividenden am linken Teppichrand aus und ordnet entsprechend die Marken darunter. Der Divisor wird hier mit einem blauen 10er-Kegel und zwei grünen 1er-Kegeln dargestellt.

Beginnend bei den 1000ern werden die Plättchen nun gerecht verteilt! Achtung: Der blaue Kegel bekommt immer 10 mal so viel wie jeweils ein grüner Kegel! Blau bekommt einen 1000er, grün bekommt dementsprechend je einen 100er usw. (siehe PDF).

Können Marken des Dividenden nicht mehr gerecht an alle Kegel eines Stellenwertes verteilt werden, muss gegen den nächstkleineren Stellenwert bei der Bank getauscht werden (siehe Goldene Perlen - Division).

Mehrstelliger Divisor mit Nullstellen:

Die Aufgabe lautet zum Beispiel 3468 : 204. Das Kind legt wie gehabt den Dividenden am linken Teppichrand mit Kartensatz und Marken aus. Im Kasten des Markenspiels befinden sich neben den Marken und Kegeln auch kleine Plättchen in den Farben der Stellenwerte. Ein Plättchen kommt anstelle des Kegels, wenn im Divisor eine Nullstelle enthalten ist. Achtung: Das Plättchen bekommt KEINE Marken, zählt aber als Stellenwert! Das heißt, bekommt der rote 100er-Kegel einen 1000er wird dem 1er-Kegel enstprechend nur ein 10er zugeordnet.

Kleiner Rechenrahmen

Ziele:

Abstrakte Zahldarstellung / Erkennen der Stellenwerte und Üben der Übergänge / Zählen und Aufschreiben von dargestellten Zahlen des Rechenrahmens / Addieren und Subtrahieren ein- bis vierstelliger Zahlen

Einführung:

Wie beim Markenspiel gelingt die Loslösung vom konkreten Material am besten mit den goldenen Perlen. Neben dem am Arbeitsplatz bereitgestellten Rechenrahmen lege ich den 1000er, den 100er, den 10er sowie den 1er des GPMs. "Gib mir mal den 1er! - Genau, das ist ein 1er ..." ich verschiebe am Rechenrahmen einen 1er nach rechts "... und das ist auch einer 1er." Ich schiebe den 1er wieder zurück. Mit den anderen Stellenwerten verfahre ich genauso.

Material: Montessori Lernwelten (Werbung)

Die Einführung erfolgt in der Drei-Stufen-Lektion.

Nun werden die Stellenwerte durchgezählt. Ich zähle und schiebe am Rechenrahmen: "Ein 1er, zwei 1er, drei 1er ..." Das Kind führt fort. Bei zehn 1ern frage ich: "Du weißt noch, was bei zehn passiert?" -> Tauschen! "Genau!" Ich tausche die zehn 1er gegen einen 10er, schiebe die zehn 1er-Perlen nach links und gleichzeitig (!) eine 10er-Perle nach rechts. Nun werden die 10er gezählt. "Ein 10er, zwei 10er, drei 10er ..." Das Kind übernimmt. Wie bei den 1ern, werden die zehn 10er gegen einen 100er getauscht. Mit den 100ern und 1000ern verfahre ich genauso.

Aufschreiben der Stellenwerte:

"Das wollen wir mal aufschreiben!" Ich zeige dem Kind das Formular zum kleinen Rechenrahmen und frage das Kind: "Zeige mir mal die 1er auf dem Rechenrahmen." Das Kind zeigt die 1er und ich zeige dem Kind die einer auf dem Formular. "Durch diese Spalte ziehen wir auch eine grüne Linie, da die 1er grün sind." Erneut beginnt das Kind zu zählen und schreibt jeweils die Zahlen auf die grüne Linie des Formulars. Bei zehn wird gestoppt. Wieder werden zehn 1er gegen einen 10er getauscht. Nun wird ein blauer Strich gezogen. Das Kind zählt die 10er und schreibt auf. Genauso verfahre ich mit den übrigen Stellenwerten.

Achtung: Die Nullstellen werden noch nicht aufgeschrieben!

Auf einem zweiten Formular werden die Nullstellen eingeführt. Wieder zählt das Kind und wechselt zehn 1er gegen einen 10er. "Wie viele Einer stehen neben einem 10er?" -> Keine. "Genau, also Null." Ich schreibe die Null in das Formular und das Kind führt das Aufschreiben der Stellenwerte fort. Der Wert der Null wird hier verdeutlicht!

Übungen:

Zahlen auf dem Rechenrahmen einstellen und das Kind überträgt die Zahlen in ein Formular. Zahlen im Formular werden vom Kind auf dem Rechenrahmen eingstellt.

Vorbereitete Aufgabenkärtchen sowohl mit Zahlen als auch mit Abbildungen eines Rechenrahmens.

Addieren von vierstelligen Zahlen (mit Ergebnis im vierstelligen Bereich!):

1. Ohne Nullstellen und Umtäusche

Ich schreibe eine Zahl (z.B. 2734) in das Formular und das Kind stellt diese ein. Ich ergänze das Formular mit einer weiteren Zahl und sage: "Diese Zahl zählen wir jetzt dazu." (Ich schreibe ein + vor die Zahl, z.B. + 5241.) "Wie viele 1er kommen hinzu?" -> 6, ich achte darauf, dass das Kind die Stellernwerte einzeln zählt - "Ein 1er, zwei 1er ... sechs 1er." - "Wie viele 10er / 100er / 1000er kommen hinzu?" Das Kind nennt das Ergebnis und schreibt dieses in das Formular.

Übungen:

- Vorbereitete Aufgabenkarten (Lösung rückwärtig)

- Aufschreiben der Aufgaben in das bekannte Formular

- Aufgaben mit mehreren Summanden

Demonstration (HD 1080p):

2. Mit Umtäuschen

Wieder schreibe ich zwei Zahlen in das Formular, diesmal mit 10er-Überschreitung, z.B. 3389 + 2745. Das Kind stellt die erste Zahl auf dem Rechenrahmen ein. Danach übernehme ich und führe die Aufgabe einmal bis zum Ergebnis durch. Ich zähle laut: "Ein 1er, ... ich tausche ... zwei 1er, dre 1er ...!" Beim Tauschen von zehn 1er gegen einen 10er achte ich darauf, dass ich die 1er Perlen gleichzeitig nach links schiebe, während ich einen 10er nach rechts schiebe und danach gleich den vierten 1er anschließe. Achtung, das Kind neigt dazu, beim Tauschen weiter zu zählen, daher ist das Vormachen durch die Lehrerin hier besonders wichtig! Wieder zähle ich laut: "Ein 10er ... ich tausche ... zwei 10er, drei 10er, ..." Gleichzeitiges Tauschen von zehn 10ern gegen einen 100er. Mit den 100ern und 1000ern verfahre ich genauso. Auch hier nennt das Kind das Ergebnis und schreibt dieses in das Formular.

Übungen:

- Vorbereitete Aufgabenkarten (Lösung rückwärtig)

- Aufschreiben der Aufgaben in das bekannte Formular

- Aufgaben mit mehreren Subtrahenden

Demonstration (HD 1080p):

Subtrahieren von vierstelligen Zahlen:

1) Ohne 10er-Unterschreitung

Ich schreibe dem Kind eine Aufgabe in das Formular, z.B. 4675-3243. "Was passiert beim Subtrahieren noch mal?" -> Ich nehme etwas weg! "Genau, von der ersten Zahl wollen wir die zweite Zahl abziehen / wegnehmen. Stelle mal die obere Zahl auf dem Rechenrahmen ein." Das Kind stellt die Zahl dar und schiebt die Perlen in ihren Stellenwerten nach rechts. "Subtrahieren heißt wegnehmen, also nehmen wir drei 1er wieder weg." Ich schiebe drei 1er zählend nach links. Das Kind kann ab hier übernehmen. "Das Ergebnis ist das, was übrig bleibt!" Das Kind nennt das Ergebnis und schreibt es in das Formular.

2) Mit 10er-Unterschreitung

In das Formular schreibe ich 7482-3735. Die erste Aufgabe der Subtraktion mit 10er-Unterschreitung führe ich komplett vor, nachdem das Kind den Minuend eingestellt hat. Ich schiebe von rechts nach links: "Ein 1er, zwei 1er ... ich tausche ... drei 1er, vier 1er, fünf 1er." Beim Tauschen schieben ich zehn 1er nach rechts und gleichzeitig einen 10er nach links. So fahre ich mit 10er , 100ern und 1000ern fort.

Demonstration (HD 1080p):

Großer Rechenrahmen

Ziele:

Addieren , Subtrahieren , Multiplizieren bis in den Millionenbereich / stellenwertgerechtes Rechenen (Vorbereitung auf schriftliches Rechnen)

Einführung:

Mit dem Kind werden die Materialien der Hierarchie der Zahlen an den Arbeitsplatz geholt. Vom grünen 1er-Würfel bishin zum grünen 1.000.000er-Würfel werden die Materialien mit den Perlen verglichen: 1er-Würfel (grün) = 1er-Perle (grün) / 10er-Stäbchen (blau) = 10er-Perle (blau) ... usw.. Das Kind schiebt entsprechend des Materials der Hierarchie jeweils eine Perle am Rechenrahmen nach rechts.

Material: Montessori Lernwelten (Werbung)

Multiplizieren mit einstelligem Multiplikator OHNE Umtäusche:

Die Aufgabe lautet zum Beispiel 213.432 x 2. "Wir beginnen mit den 1ern - 2 x 2 ist gleich ...?" -> 4. Das Kind schiebt auf dem Rechenrahmen vier 1er nach rechts. "Gut, nun nehmen wir den 10er mal zwei - 3 x 2 ist gleich ...?" -> 6. "Genau, schiebe nun sechs 10er nach rechts." Das Kind rechnet die Aufgabe alleine zuende.

Demonstration (HD 1080p):

Multiplizieren mit einstelligem Multiplikator MIT Umtausch:

Die Aufgabe lautet zum Beispiel 172891 x 4. "Wir beginnen mit den 1ern - 1 x 4 ist gleich ...?" -> 4. Das Kind schiebt auf dem Rechenrahmen vier 1er nach rechts. "Gut, nun nehmen wir den 10er mal vier - 4 x 9 ist gleich ...?" -> 36. "Genau, das sind am Rechenrahmen sechs 10er und drei 100er." Ich rechne und schiebe die Aufgabe zuende.

Demonstration (HD 1080p):

Übungsbeispiel:

Mit diesen kleinen Blöcken (hier von Johanna Rössler - Werbung) üben die Kinder die Addition (Holen) sowie die Subtraktion (Bringen) am großen und kleinen Rechenrahmen.

Zum Beispiel hier (Fotos) die Addition - Seite für Seite werden Zahlen am Rechenrahmen addiert und am Ende müssen die Perlen mit der letzten Zahl im Büchlein übereinstimmen.

Beim Subtrahieren startet das Kind mit 999.999, stellt die Perlen am Rechenrahmen ein und nimmt Seite für Seite die Perlen entsprechend der Zahlen weg. Auch hier müssen die Perlen mit der letzten Zahl im Büchlein übereinstimmen.

Große Multiplikation (Schachbrett)

Ziele:

Multiplizieren großer Zahlen, auch mit mehrstelligem Multiplikator / Einmaleinskenntnisse üben und sichern / Hinführung zur schriftlichen Multiplikation

Hinführung:

Dem Kind sind die Farben der Stellenwerte bekannt. "Grün steht für 1er, daher ist das grüne Feld das 1er-Feld." Ich zeige auf das grüne Feld rechts unten. "Blau steht für 10er. Die blauen Felder sind daher 10er-Felder." Ich zeige auf die beiden blauen Felder links und oberhalb vom 1er-Feld. Ebenso verfahre ich mit dem roten 100er-Feld und allen weiteren Stellenwerten. Die Bezeichnung der Felder wird über die Drei-Stufen-Lektion eingeführt, sofern das Kind diese noch nicht kennt. 

Nun lege ich (z. B.) ein 4er-Stäbchen in das untere rechte 1er-Feld und sage "Das sind vier 1er." Ich schiebe das Stäbchen ein Feld nach links. "Das sind vier 10er." Ich schiebe das Stäbchen ein weiteres Mal nach links. "Das sind vier 100er." Die Bilder zeigen das Verschieben des 4er-Stäbchens. An dem Multiplikationsbrett wird gerne gearbeitet, wie unschwer zu erkennen ist.

Wieder lege ich das Stäbchen ind das 1er Feld ganz unten rechts und lasse das Kind die Zahl nennen. Ich schiebe das Stäbchen ein Feld nach oben. "Kannst du auch hier den Wert nennen?" -> Vier 10er. So benennt den Perlenwert der darüberliegenden Felder.

Auch das die Felder im diagonalen Verschieben ihren Stellenwert nicht ändern mache ich mit dem 4er-Stäbchen vor. Nach Bekanntmachung aller Felder mit ihren Stellenwerten lege ich das Stäbchen an eine beliebige Stelle und lasse das Kind die Zahl benennen (auch mit verschiedenen farbigen Stäbchen).

Zahlen darstellen und benennen

Ich lege eine Zahl mit Stäbchen und lasse das Kind die Zahl benennen. Am Anfang helfen die "Familiennamen" der 100, 1000 und 1.000.000.

Multiplizieren

Das Multiplizieren kann in drei Phasen stattfinden. Für Phase 1 ist es nicht Voraussetzung, dass das Kind das Einmaleins beherrscht, da nur additiv gerechnet wird. Phase 2 und 3 setzt die Fähigkeit des Kindes voraus, das kleine Einmaleins im Kopf rechnen zu können. Es ist nicht zwingend notwendig, das Schachbrett mit der ersten Phase einzuführen, wenn das Kind das kleine Einmaleins schon beherrscht.

Phase 1

(Beispiel mit einstelligem Multiplikator und ohne Stellenwerttausch)

Phase 2

(Beispiel mit einstelligem Multiplikator und mit Stellenwerttausch)

Phase 3

(Beispiel mit zweistelligem Multiplikator und Stellenwerttausch)

...folgt...

Liegender Rechenrahmen

Ziele:

Multiplizieren von Aufgaben (bis vierstelligem Multiplikator) / Hinführung zum schriftlichen Rechenverfahren

Voraussetzung:

Auch hier muss das Kind sicher im kleinen 1x1 sein. Am Schachbrett hat das Kind bereits Aufgaben mit mehrstelligem Multiplikator kennengelernt.

Einführung von Stufenzahlen:

Ich zeige dem Kind den liegenden Rechenrahmen und frage es nach bekannten Merkmalen. -> Markierung der Stellenwerte in weiß, grau und schwarz, wie beim großen Rechenrahmen. "Genau. Und was ist anders?" -> Die Perlen sind alle golden. Ich öffne die Box: "Die weißen Plättchen sind für die Zahl, die wir malnehmen wollen, den Multiplikanden, und werden hier unten hingelegt." Ich lege (z.B.) die Zahl 4643 entsprechend auf die Nullen und decke diese somit ab. "Die grauen Plättchen sind für die Zahl mit welcher wir malnehmen, den Multiplikator, und diese legen wir an den rechten Rand entsprechend ihres Wertes." Ich lege (z.B.) die Zahl 2 auf den grünen 1er-Punkt (1. Bild). Nun ist die Aufgabe mit den Plättchen gelegt. "Wir nehmen den 1er mal." Ich lege das graue Plättchen OBEN auf den Stellenwert des 1er (Bild 2) und sage: "2x3 = 6." Danach schiebe ich sechs goldene Perlen nach unten. Das graue Plättchen wandert auf den Stellenwert des 10er (Bild 3): "2x4 = 8." Ich schiebe acht goldenen Perlen nach unten. Das graue Plättchen wandert auf den Stellenwert des 100er (Bild 4): "2x6 = 12." Ich schiebe zwei 1er (zwei goldene Perlen beim Stellenwert des 100er) und einen 10er (eine goldene Perle beim Stellenwert des 1000er). So fahre ich fort bis alle weißen Plättchen einmal mit dem grauen Plättchen multipliziert wurden (Bild 5). Zum Schluss liest das Kind das Ergebnis auf dem liegenden Rechenrahmen ab und kontrolliert (Bild 6).

Material: Nienhuis (Werbung)

Die nächste Aufgabe erfolgt mit gleichem Multiplikanden mal 20 - das graue Plättchen mit der grünen 2 wird durch ein graues Plättchen mit einer blauen 2 getauscht und auf den blauen Punkt gelegt. Auf den nun verbleibenden grünen 1er-Punkt wird ein graues Plättchen mit einer grünen Null gelegt (Bild 1). Wie oben wird zuerst mit dem 1er multipliziert. Da alles mal Null genommen wird, werden keine goldenen Perlen nach unten geschoben. Nun wird das graue Plättchen mit der Null umgedreht und wieder auf seinen grünen Punkt gelegt. Es wird mit dem 10er multipliziert (der blauen 2) - dafür wird die 4643 auf den weißen Plättchen jeweils einen Stellenwert nach links gerückt (Bild 2). Nun ist unten die Zahl 46430 zu sehen, welche auf nun bekannte Weise mit der 2 multipliziert wird. Das Kind nennt das Ergebnis, kontrolliert (Bild 3) und kann nun die Aufgabe bis 2000 alleine weiterführen.

Große Division (Apotheke)

Ziele:

Dividieren bis in den Bereich der Million (Dividend) mit 1- bis 4-stelligem Divisor

Hinführung:

Gemeinsam wird das Material auf den Arbeitsteppich geholt. Den großen Rechenrahme nehme ich mit und frage das Kind: "Den Rechenrahmen kennst du ja schon. Fällt dir hier was auf?" -> Kind nennt die Farbverteilung von weiß / grau / schwarz und kann diese den Stellenwerten zuordnen. Das Kind ordnet die Ständer mit den Perlen sowie die passenden Schälchen zu.

Darstellen und Benennen einer Zahl:

Das Kind stellt aufgeschriebene Zahlen dar, indem es die entsprechenden Perlen aus den Reagenzgläschen in das davor liegende Schälchen legt. Im Beispiel die Zahl a) 10.327 und die Zahl b) 5.291.683.

Umgekehrt schreibt das Kind eine mit Perlen dargestellte Zahl auf. An dieser Stelle ist es nicht mehr wichtig, dass die Zahlen in den Stellenwertfarben grün, blau und rot aufgeschrieben werden. Als Orientierung kann eine Tabelle dienen, in der M / HT / ZT / T / H / Z / E farbig hervorgehoben sind.

Divison mit einstelligem Divisor (ohne Rest):

Ich schreibe eine Divisionsaufgabe auf, die Aufgabe lautet (z.B.) 9365 : 5. Ich frage das Kind, auf wie viele die Perlen verteilt werden müssen. -> auf fünf. "Genau!" - ich lege das grüne Divisionsbrett auf den Teppich - "Stelle mal fün grüne Figuren oben auf das Feld. Das kennst du ja schon." (Abb. 1) Die Ständer bis 1000 sowie die dazu passenden Schälchen werden auf den Arbeitsteppich gelegt, die nicht benötigten Ständer und Schälchen bleiben auf dem Tablett (deutlich an der Seite). (Abb. 2)

Ich rufe in Erinnerung: "Das Ergebnis einer Division ist das ..." -> was einer bekommt. "Gut. Verteile nun die grünen Perlchen gerecht." Es können fünf Perlen zugeordnet werden, vier bleiben übrig und können so nicht mehr verteilt werden. Die verbleibenen vier Perlen werden gegen vier 10er-Gläschen der roten Perlen getauscht: die roten Perlen kommen ins rote Schälchen, die vier grünen Perlen kommen zurück in ein Gläschen. "Wie viel bekommt einer?" -> einen. "Gut, das schreiben wir auf!" (Hierfür können vorbereitete Formulare bereit liegen, in welche schon zuvor die Aufgabe geschrieben wurde.) Danach werden die grünen Perlen abgeräumt und kommen zurück in das Gläschen.

Abb. 1 zeigt die verbleibenen 4 grünen Perlen, Abb. 2 die eingetauschten roten Perlen, welche nun über das Divisionsbrett geschoben werden. Der nicht mehr benötigte 1000er-Ständer wird deutlich zur Seite geschoben und das Schälchen umgedreht.

Wieder werden alle roten Perlen gerecht auf die Figuren verteilt. Es bleiben drei rote Perlen übirg, welche nun gegen drei 10er-Gläschen mit blauen Perlen getauscht werden. Die roten Perlen kommen zurück in ein Gläschen, die 30 blauen Perlen in das blaue Schälchen. "Wie viel bekommt einer?" -> Acht. Das Teilergbnis wird aufgeschrieben. (Abb. 1)

Die roten Perlen werden abgeräumt (Ständer und Schälchen werden wieder deutlich zur Seite gestellt) und der Ständer sowie das Schälchen mit den blauen Perlen kommen über das grüne Divisionsbrett. (Abb. 2)

Nun werden alle blauen Perlen gerecht auf die Figuren verteilt. Es bleibt eine blaue Perle übirg, welche nun gegen ein 10er-Gläschen der grünen Perlen getauscht wird. Die blaue Perle kommt zurück in ein Gläschen, die 10 grünen Perlen in das grüne Schälchen. "Wie viel bekommt einer?" -> Sieben. Das Teilergebnis wird aufgeschrieben. (Abb. 1)

Die blauen Perlen werden abgeräumt und der Ständer sowie das Schälchen mit den grünen Perlen kommen nun über das grüne Divisionsbrett. (Abb. 2)

Division mit zweistelligem Divisor (ohne Rest):

Ich schreibe eine Divisionsaufgabe auf, die Aufgabe lautet (z.B.) 70770:42. "Auf wie viele müssen wir verteilen?" -> auf 42. "Gut." - ich lege das grüne Divisionsbrett für die 1er und das blaue Divisionsbrett für die 10er (links neben das grüne Brett) auf den Arbeitsteppich. "Wie viele grüne Figuren kommen auf das grüne Brett?" -> zwei. "Und wie viele blaue Figuren kommen auf das blaue Brett?"-> vier. Danach stellt das Kind den Divididenden mit den Perlen dar und räumt die nicht benötigten Ständer und Schälchen deutlich zur Seite.

Wieder wird mit den hohen Stellenwerten begonnen. Ständer mit blauen Perlen und blaues Schälchen kommen über das blaue Brett, die grünen über das grüne Brett. (Abb. 1) "Eine blaue Figur hat den gleichen Wert wie zehn grüne Figuren. Eine blaue Perle hat den gleichen Wert wie zehn grüne Perlen. Für jede Perle die bei den blauen Figuren gelegt werden, muss gleichzeitig eine grüne Perle bei den grünen Figuren gelegt werden." Das Kind sieht, dass es in diesem Falle gleich eine blaue Perle gegen zehn grüne Perlen tauschen muss. Die blaue Perle kommt ins Gläschen, die grünen Perlen in das grüne Schälchen. Die Perlen werden verteilt und das Teilergbnis, was einer bekommt, wird notiert. (Abb. 2)

Die verbleibenen blauen Perlen werden (hier) gegen zwei 10er-Röhrchen getauscht, welche in die grüne Schale kommen. Alle Perlen auf den Brettern werden abgeräumt und kommen zurück in die Gläschen, der 10.000er-Ständer wird deutlich zur Seite geschoben und das blaue Schälchen umgedreht davor gelegt.

Der 1000er-Ständer samt Schälchen wird nun über das blaue Divisionsbrett geschoben und der 100er-Ständer mit den roten Perlen und seinem Schälchen liegt nun über dem grünen Divisionsbrett. (Abb. 1)

Die Perlen werden wieder verteilt: für jede grüne Perle die auf das blaue Brett gelegt wird, wird eine rote Perle auf das grüne Brett gelegt, so lange, wie alle blauen Figuren auch eine Perle bekommen (auch hier muss eine grüne Perle gegen zehn rote Perlen getauscht werden). "Wie viel bekommt einer?"- sechs. Das Teilergebnis wird notiert. (Abb. 2)

Die verbleibenen grünen Perlen werden gegen drei rote Perlengläschen getauscht, dann werden die grünen und roten Perlen auf den Brettern abgeräumt und der 1000er-Ständer wird deutlich zur Seite gelegt (Schälchen umdrehen).

Nun kommt der Ständer mit den roten Perlen über das blaue Brett und der Ständer mit den blauen Perlen über das grüne Brett. Die Verteilung der Perlen erfolgt wie beschrieben. (Abb. 1) Ist das Teilergebnis notiert, werden die verbleibenen Perlen getauscht, die Bretter abgeräumt und der letzte Ständer über das grüne Brett gezogen. Ein letztes Mal erfolgt die Verteilung der Perlen. Bei einer Aufgabe ohne Rest darf keine Perle im Schälchen übrig bleiben. (Abb. 2)

Das Teilergebnis wird aufgeschrieben und das Gesamtergebnis vorgelesen.

Das Kind kann selbstständig Aufgaben mit zweistelligem Divisor ohne / mit Rest rechnen (Aufgabenkarten).

Aufgaben mit vierstelligem Divisor (ohne Rest):

Die Aufgabe lautet: 7.147.770 : 4.242

Entsprechend der vier Stellenwerte des vierstelligen Divisors werden auch alle vier Divisionsbretter benötigt. Auch hier gilt: Für jede grüne 1000er-Perle muss auch eine rote 100er-, eine blaue 10er- sowie eine grüne 1er-Perle gelegt werden können! Es wird so lange wie gehabt getauscht, bis grüne 1000er-Perlen nicht mehr gerecht auf alle grünen Figuren verteilt werden können.

Das Kind kann nun selbständig im Bereich der Million mit einem bis zu vierstelligem Divisor rechnen (Aufgabenkarten).