Montessori-Material zu den Grundaufgaben
Schlangenspiel zur Addition
Streifenbrett zur Addition
Additionstabellen
Schlangenspiel zur Subtraktion
Streifenbrett zur Subtraktion
Subtraktionstabellen
Perlenstäbchen zur Multiplikation
Kleines Multiplikationsbrett
Multiplikationstabellen
Divisionsbrett
Divisionstabellen
Ziele:
Zählendes Addieren von Einern / 10er-Zerlegung
Vorbereitung:
Zusammen mit dem Kind hole ich das Material zum Schlangenspiel und stelle das Tablett mit den Kästchen auf den Arbeitsteppich. Ich kippe die schwarz-weißen Perlen aus und beginne zu sortieren (in Anlehnung an die farbigen Perlen). Durch die schwarz-weißen Perlen bleibt die "Kraft der Fünf" erhalten (5 Perlen schwarz, danach weiß). Nach der 3 kann das Kind übernehmen - ggf. helfe ich, wenn die weißen Perlen beginnen.
Ich öffne die Box mit dem roten Deckel. "Lege mal mit den bunten Perlen eine lange bunt gemischte Schlange!" (Bei Bedarf zeige ich eine gewünschte Länge an.) Ist das Kind fertig, schließe ich die rote Box und stelle sie zur Seite.
Einführung:
Ich öffne die Box mit dem "goldenen" Deckel (10er Stangen) und stelle sie bereit. Mit einem Reiterchen zähle ich nun laut die ersten 10 Perlen der bunten Schlange ab. Das Reiterchen bleibt hinter der 10. Perle stecken. "Für 10 Perlen kann ich auch ein 10er Stäbchen nehmen!" Ich nehme einen 10er und lege diesen ÜBER die abgezählten farbigen Perlen. Mit dem Reiterchen zähle ich nun laut das "angebrochene" Stäbchen zu Ende. Entsprechend der restlichen Perlen lege ich das passende schwarzweiße Stäbchen dazu. "Den Rest legen wir mit den schwarz-weißen Perlen." Nun öffne ich die Box mit dem weißen Deckel und lege die farbigen Stäbchen VOR und MIT dem Reiterchen in die Box. Wieder beginne ich am linken Ende der Schlange zu zählen (nun beginnt diese mit dem schwarzweißen Stäbchen) und zähle bis 10. Abhängig vom Kind, kann an dieser Stelle schon übernommen werden. Achtung: die schwarzweißen Stäbchen kommen zurück in die Ordnung der schwarz-weißen Stäbchen! Nur farbige Stäbchen wandern in die Box.
Nach immer gleichem Prinzip wird die bunte Schlange durchgezählt bis alle Stäbchen der Schlange komplett in der Box liegen und durch 10er ersetzt wurden. Meist bleibt am Ende ein schwarzweißes Stäbchen übrig, welches dann liegen bleibt.

Die Stäbchen werden nun in bekannter Weise vom Kind geordnet und gezählt. Ich nehme die Box mit den gesammelten bunten Stäbchen der Schlange und schütte sie auf dem Arbeitsteppich aus.
"Nun müssen in der Box ja genauso viele Stäbchen sein, wie du hier gezählt hast. Sortiere die doch auch mal." Das Kind ordnet die farbigen Perlen zur bekannten Ordnung der Pyramide an.
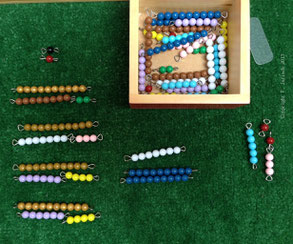
Ich nehme das erste 10er-Stäbchen, lege es waagerecht hin und sage: "10 ist 8 plus 2." Unter das 10er-Stäbchen lege ich das 8er- und 2er-Stäbchen. Das Kind führt die 10er-Zurodnung fort. Ist es noch nicht sicher in der 10er-Zerlegung, zählt es mit dem Reiterchen immer 10 an den farbigen Stäbchen ab. Bleiben, wie im Beispiel zu sehen, Stäbchen übrig, die nicht mehr zu einem 10er zusammengelegt werden können, muss bei der "Bank" (der roten Box) gewechselt werden - hier: ein 5er-Stäbchen gegen zwei 1er-Stäbchen und ein 3er-Stäbchen.

Fehlerkontrolle:
Sind alle farbigen Stäbchen den 10ern zugeordnet und verbleibt genau ein farbiges Stäbchen passend zum schwarz-weißen Stäbchen wurde richtig zusammengezählt.
Zählen:
Beim Schlangenspiel kann auf unterschiedliche Weise gezählt werden. Entweder fortlaufend (1, 2, 3, ... 10) oder das Kind (welches den Wert der einzelnen Stäbchen schon kennt), beginnt das Zählen mit dem Wert des vorliegenden Stäbchens: "5 - 6, 7, ... 10"
Addieren:
Das Kind kann zählend addieren (5 ... 6, 7, 8, 9, 10) oder kann die Werte der Stäbchen gleich zusammen zählen und mit dem 10er und dem entsprechenden schwarzweißen Stäbchen legen (5+7=12 -> Kind legt 10+2).
Ziele:
Üben und Festigen der Grundaufgaben der Addition / Summandenzerlegung / Tauschaufgaben / bis zur 10 ergänzen / 10er-Überschreitung
Vorbereitung:
Ich lege das Streifenbrett der Addition (1-10 rot!) auf den Arbeitsteppich und verteile die blauen Streifen unsortiert auf der linken sowie die roten Streifen unsortiert auf der rechten Seite des Bretts.
Nun beginne ich die blauen Streifen zu sortieren und zähle dabei: "1". Die 1 kommt an den linken oberen Rand des Bretts. "2" - die 2 lege ich darunter. In der Regel kann das Kind ab hier übernehmen. Genauso verfahre ich mit den roten Streifen und beginne diese am rechten Rand des Bretts zu sortieren.
Material: Montessori Lernwelten (Werbung)
Einführung:
Auf das Streifenbrett lege ich eine Plusaufgabe, z.B. 4+3. Die blaue 4 liegt links, daneben liegt die rote 3. Beim Legen sage ich: "4 plus 3 ist gleich ...?" Das Kind kann das Ergebnis auf dem Streifenbrett ablesen (ggf. zeige ich mit dem Finger auf die 7) und sagt "sieben". Nun ist das Kind an der Reihe eine Aufgabe zu legen. Dann sage ich dem Kind eine Aufgabe, es legt ist und nennt das Ergebnis.
Üben der Grundaufgaben:
- Aufgabenkärtchen (durcheinander)
- Grundaufgabenheftchen: Aufbau von Additionsreihen (siehe Bild) - das Kind legt die blaue 1 und die rote 1, dann die blaue 1 und die rote 2 usw.. Das Ergebnis wird in das Heftchen eingetragen und kann mit der Kontrolltafel verglichen werden.
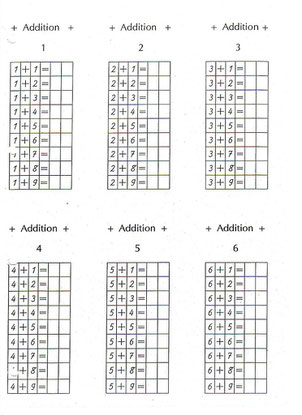
So kann ein Grundaufgabenheft aufgebaut sein. Der einzige Nachteil an vorbereiteten Heftchen ist, dass ein Kind immer das Gefühl hat "fertig werden zu müssen" und auch der Pädagoge sich schwer davon frei machen kann, ein unbeendetes Heftchen zu tolerieren. :)
In der Montessori-Pädagogik ist es eigentlich nicht vorgesehen, mit etwas fertig zu werden, weil das Material Grenzen setzt. Vielmehr ist das Kind dann fertig, wenn es beschließt aufzuhören.
Wir führen die Grundaufgabenhefte dennoch, da es viele Kinder gibt, die es lieben, genau so ein Heftchen auch fertig zu bekommen.
Systematische Analyse der Grundaufgaben:
- Alle Aufgaben mit gleichem Ergebnis
"Finde alle Aufgaben mit dem Ergebnis (z.B.) 7." Ich beginne und lege 6+1. Das Kind kann ab hier übernehmen. Die Aufgaben bleiben liegen, da ja ALLE Aufgaben gefunden werden sollen.
- "+0" zu Aufgaben mit gleichem Ergebnis
Ist das Kind oben nicht auf 7+0 gekommen, bitte ich das Kind nun z.B. alle Aufgaben zu legen, deren Ergebnis 9 ist. Zum Schluss lege ich die 9 und sage: "9 plus ..." und schiebe gestisch nichts rüber. Das Kind kennt dies von den Spindeln und sagt "null".
- Paare finden
Ich schiebe die Streifen zu 9+0 nach oben und bitte das Kind die ähnliche Aufgabe zu finden. Das Kind legt 0+9 und ich schiebe es unter die Streifen 9+0. Nun werden alle Paare gesucht und zueinander gelegt. So verfahre ich mit allen Zahlen von 1 bis 9.
- Tauschaufgaben
Nun schiebe ich das Paar 9+0 / 0+9 wieder nach unten und frage das Kind, was einfacher zu rechnen ist. Höchstwahrscheinlich wird das Kind "9+0" nennen. "Genau. Diese Aufgaben kann man tauschen und nennt man deshalb Tauschaufgaben. Und weil beide Aufgaben das gleiche Ergebnis haben, lassen wir die einfache liegen und sortieren die, die dir schwerer erschien, wieder an den Rand." So verfährt das Kind mit den weiteren Paaren. Zur Kontrolle bietet sich hier die "halbe Kontrolltafel" an. Auf dieser sind jedoch nur die "schweren" Aufgaben zu finden, damit das Kind gleich zum Tauschen angeregt wird.
- Gleiche Summanden / gerade und ungerade
Ich lege auf das Brett die blaue und die rote 1 und frage: "1+1 sind ...?" Das Kind nennt 2. Nun lege ich die blaue und die rote 2 und frage: "2+2 sind ...?" - 4. Das Kind kann ab hier übernehmen. Das Kind wird feststellen, dass das Ergebnis immer im 2er-Schritt größer wird und gerade ist, egal ob die Summanden gerade oder ungerade waren. Hier kann ich erweitern, indem ich dem Kind mit den Streifen zeige, dass gerade+gerade sowie ungerade+ungerade gleich "gerade Zahl" ist, dass aber ungerade+gerade immer gleich "ungerade Zahl" ist.
- Überschreiten der 10
"Lege mal folgende Aufgabe, die ich dir auf einen Papierstreifen schreibe." Ich nehme z.B. die Aufgabe 7+4. Kind legt die blaue 7 und die rote 4. "Gut. Und nun zählen wir wie beim Schlangenspiel bis zur 10! Wie viel sind es bis zur 10?" Das Kind nennt "3". "Und wie viel bleibt dann noch bis zur 11?" - 1. Hier ist die Unterteilung der roten Streifen in Einerkästchen wichtig, da das Kind so zählen kann. Auf einen weiteren Papierstreifen schreibe ich 7+3+1=11. Wenn das Kind gut in der Übung ist, kann 7+3 auch schon zu 10 zusammengefasst werden, so dass nur noch 10+1=11 aufgeschrieben wird.
Ziele:
Üben und Festigen der Grundaufgaben der Addition / Tauschaufgaben

Kontrolltafeln
Die erste Kontrolltafel enthält alle Lösungen der Addition im Bereich der Grundaufgaben.
Wie oben beschrieben, gibt es neben der vollen Kontrolltafel auch die halbe Kontrolltafel. Hier sind alle "einfachen" Tauschaufgaben nicht mehr abgebildet. Das Kind wird so indirekt aufgefordert sofort die einfache Tauschaufgabe zu bilden, um schnell zur Lösung zu kommen.
Die Kontrolltafel dient der selbstständigen Fehlerkontrolle.

Additionstabellen
Es gibt vier Additionstabellen, mit welchen das Kind alle Grundaufgaben der Addition üben und kontrollieren kann:
- Der rechte Zeigefinger liegt auf dem 1. Summanden im blauen Bereich, der linke Zeigefinger auf dem 2. Summanden im roten Bereich. Die Finger bewegen sich senkrecht und waagerecht aufeinander zu und treffen sich im Ergebnis. Das Kind übt hier Grundaufgaben (z.B. mit Aufgabenkärtchen) und kann mit der Kontrolltafel 1 überprüfen.
- Der rechte Zeigefinger liegt auf dem kleineren Summanden im roten Bereich und der linke Zeigefinger auf dem höheren Summanden, ebenfalls im roten Bereich. Der rechte Zeigefinger fährt waagerecht bis an den rechten Rand und dann senkrecht runter bis zur Zahl des linken Zeigefingers. Dieser bewegt sich dann waagerecht auf den rechten Zeigefinger zu - wo sie aufeinandertreffen ist das Ergebnis. Das Kind übt hier die Tauschaufgaben (z.B. mit Aufgabenkärtchen) - es stellt fest, dass die Fingerbewegungen die gleichen sind, egal ob 8+4 oder 4+8, und auch das Ergebnis das gleiche ist. Mit der Kontrolltafel 2 kann überprüft werden.
- Die dritte Additionstabelle bedarf einiger Übung! Wieder liegt der rechte Zeigefinger auf dem kleineren Summanden und der linke auf dem größeren Summanden im roten Bereich (Aufgabenkärtchen). Beide Zeigefinger fahren waagerecht bis an den rechten Rand. Nun bewegen sich beide Zeigefinger aufeinander zu (optimal im Zeigefinger- / Daumensprung). Ist das Ergebnis gerade, treffen sich die Finger beider Hände in dem Feld des Ergebnisses. Ist die Zahl ungerade, liegt das Ergebnis zwischen den beiden Fingern auf der inneren Diagonale. Das Kind übt und vertieft die Grundaufgaben der Addition.
- Hier sichert das Kind seine Kenntnisse im Bereich der Grundaufgaben der Addition. Wieder mithilfe der Aufgabenkärtchen löst das Kind die Aufgaben alleine und legt das Ergebnis mit den Ergebnisplättchen des kleinen roten Kästchens. Fehlerkontrolle: Alle Plättchen können gelegt werden. / Kontrolltafeln.
Material: Montessori Lernwelten (Werbung)
Ziele:
Zählendes Addieren von Einern / Zählendes Subtrahieren
Vorbereitung:
Zusammen mit dem Kind hole ich das Material zum Schlangenspiel und stelle das Tablett mit den Kästchen auf den Arbeitsteppich. Ich kippe die schwarz-weißen Perlen aus und bitte das Kind, diese zu sortieren - "Das kennst du ja schon!".
Ich öffne die Box mit dem roten Deckel. "Lege wieder mit den bunten Stäbchen eine lange bunt gemischte Schlange!" Während das Kind die Stäbchen legt, füge ich drei bis vier graue Stäbchen aus der Box mit dem grauen Deckel in die Schlange ein. Das sind die Stäbchen die später abgezogen werden sollen - ACHTUNG: es muss darauf geachtet werden, dass durch die Perlenzahl der grauen Stäbchen die Perlenzahl der bunten Stäbchen NICHT überschritten wird, da sonst ein Ergebnis unter Null rauskommen würde.
Einführung:
"Beginne mal zu zählen, bis zur 10. Du kennst das schon vom Schlangenspiel zur Addition." Das Kind zählt und legt wie bekannt die 10er-Stäbchen sowie die schwarzweißen Stäbchen und ersetzt die bunten Stäbchen. So verfährt das Kind bis zum ersten grauen Stäbchen. Ich unterbreche das Kind beim Zählen und sage: "Ich zeig dir mal was. Die grauen Stäbchen ziehen wir jetzt ab. Wir rechnen jetzt minus!" Ich lege das graue Stäbchen unter die bunten Stäbchen linkerhand und zähle sozusagen zurück: "-1, -2, -3 ..." Ist das graue Stäbchen durchgezählt wird der Rest des oberhalb liegenden 10er-Stäbchen wieder durch einen schwarzweißen Stab ersetzt. Farbige Stäbchen sowohl graue Stäbchen kommen gemeinsam in eine Box. 10er-Stäbchen kommen zurück in die Box mit dem goldenen Deckel.

Auf der Metaebene wird wie folgt gerechnet:
10 - 7 = 3
10 (hier ein 10er-Stäbchen) wird durch 7 graue und 3 schwarzweiße Stäbchen ersetzt.
10 und 7 ist "weg" und 3 bleibt als Ergebnis liegen.
Das Kind zählt weiter. Noch einmal übernehme ich bei dem nächsten grauen Stäbchen und zeige, wie man "minus zählt". Danach kann das Kind die Schlange zu Ende zählen. Mit den verbleibenden 10er-Stäbchen und dem schwarzweißen Stäbchen legt das Kind das Ergebnis.
Fehlerkontrolle:
"Du kennst das ja schon, sortiere mal die Stäbchen. Alle bunten Stäbchen und alle grauen Stäbchen." Danach fordere ich das Kind auf, zunächst den grauen Stäbchen immer passend bunte Stäbchen zuzuordnen (ggf. muss bei der "Bank" gewechselt werden). Die Perlen die nun übrig bleiben, müssen genauso viele Perlen sein, wie das Ergebnis mit den goldenen Perlen und dem schwarzweißen Stäbchen. Auch hier ordnet das Kind zu.
Ziele:
Üben und Festigen der Grundaufgaben der Subtraktion / Subtrahendenzerlegung / 10er-Unterschreitung
Vorbereitung:
Ich lege das Streifenbrett der Subtraktion (1 - 9 blau!) auf den Arbeitsteppich sowie die weißen und blauen Streifen unsortiert über das Brett bzw. rechts (!) vom Streifenbrett. Ich fange bei blau an zu zählen und zu sortieren. Wie beim schon bekannten Streifenbrett wird von oben nach unten am Rand des Brettes sortiert. Mit der "3" hat das Kind das Prinzip wieder erkannt und fährt fort zu sortieren. Ebenso verfahre ich mit den weißen Streifen. Ich nehme das längste, lege es an den oberen Rand des Bretts und sage: "1", mit dem nächstlängsten "2" und dann "3". Auch hier kann das Kind alleine weiter machen. Die weißen Streifen werden linksbündig sortiert.
Einführung:
"Nenne mir eine Zahl zwischen 1 und 18!" Das Kind nennt z.B. "7". Ich zähle die weißen Holzstreifen von unten nach oben bis zur sieben, nehme den weißen Streifen aus seiner Ordnung und bedecke die Zahlen 8-18 mit diesem Streifen. "Wie viel wollen wir von dieser Zahl abziehen / wegnehmen?" (Nennt das Kind eine Zahl über sieben, weise ich darauf hin, dass das Ergebnis bei dieser Arbeit immer zwischen 1 und 9 liegen muss, zeige dabei auf die blaue Linie nach der neun und auch in unsere erste Zahl passen muss.) Das Kind nennt nun eine weitere Zahl, z.B. "3", und ich nehme den blauen Streifen mit der 3 und bedecke die Zahlen 5-7 mit diesem Streifen. "7 minus 3 ist gleich 4!" Dabei zeige ich auf die (verdeckte) 7, fahre den 3er-Streifen lang und ende auf der 4.
Ich nenne dem Kind weitere Subtraktionsaufgaben, welche das Kind legen kann und frage es nach dem Ergebnis. Mit der Kontrolltafel kann das Kind seine Aufgabe überprüfen.
Weitere Übungen:
- eigene Aufgaben legen (und notieren)
- Aufgabenkartei bearbeiten (Fehlerkontrolle rückseitig)
- Aufgabenheftchen mit den Grundaufgaben führen - hier ist es wichtig, noch mal darauf hinzuweisen, dass nur Ergebnisse UNTER 10 aufgeschrieben werden (beginnend bei 18-9=9 ... 18-8=10 -> wird NICHT mehr aufgeschrieben / Vordruck enthält demnach nur eine Aufgabe)

Analyse der Grundaufgaben:
An dieser Stelle kommen die roten Streifen zum Einsatz, welche ich vom Kind am linken Rand des Streifenbretts der Subtraktion in die bekannte Ordnung sortieren lasse. Ich erinnere das Kind daran, dass das Ergebnis einer Grundaufgabe der Subtraktion höchstens 9 ergeben darf und zähle an den weißen Holzstreifen aufwärts bis 9. Mit dem Streifen werden nun alle Zahlen von 10 bis 18 abgedeckt.

Nun können alle Aufgaben, die 9 ergeben, gelegt werden (das Kind kennt die Zerlegung von den Additionsaufgaben):
9-9=0
9-8=1 ...
"9 minus 9 ist gleich 0." Nachdem ich den blauen Streifen mit den Fingern von rechts nach links nachgefahren bin, nehme ich ihn vom Brett und ordne ihn wieder an der Seite an. "9 minus 8 ist gleich 1." Ich verfahre genauso, die rote 1 bleibt liegen! "9 minus 2 ist gleich 7." - Wieder wird der blaue Streifen weggenommen und der rote bleibt liegen. Das Kind kann hier fortfahren. Durch das Wegnehmen der blauen Streifen bleibt der rote Streifen gut sichtbar als Differenz liegen. Hier erkennt das Kind die Umkehraufgabe zur Addition, aber auch, dass es bei der Subtraktion keine Tauschaufgaben gibt.
Ziele:
Üben und Festigen der Grundaufgaben der Subtraktion
Übungen mit den Subtraktionstabellen:
Auch bei den Grundaufgaben der Subtraktion gibt es Subtraktionstabellen (nur zwei), die in gleicher Weise gehandhabt werden wir die Tabellen 1 und 4 der Additionstabellen. In Tabelle 1 findet das Kind durch Aufeinander-Zufahren der beiden Zeigefinger das Ergebnis einer Subtraktionsaufgabe und in Tabelle 4 legt das Kind die Ergebnisse einer mit den Fingern gewählten Aufgabe mit den einzelnen Plättchen.
Mit dem großen Kasten können alle Grundaufgaben gelegt werden - aber auch Aufgaben, die nicht mehr zu den Grundaufgaben gehören, wie 18-5.
Die Kontrolltafel dient in allem als Fehlerkontrolle.
Ziele:
Aufbauen und Einprägen der Einmaleinsreihen / geometrische und dekadische Darstellung des kleinen Einmaleins
Einführung:

"Nenne mir eine Zahl zwischen 3 und 9." -> 6
Ich nehme ein 6er-Stäbchen und lege es waagerecht an den oberen linken Teppichrand. "Einmal 6! Zähl mal nach!" Das Kind zählt. "Einmal 6 ist ...?" -> 6.

Ich nehme sechs 1er-Perlen und lege sie zählend senkrecht unter das 6er-Stäbchen. Dabei lasse ich eine gute Handbreit Abstand zum waagerechten Stäbchen.

Ich lege zwei 6er-Stäbchen waagerecht rechts neben das bereits liegende 6er-Stäbchen und sage: "Das ist zweimal 6." Das Kind zählt die ausliegenden Perlen. -> Zweimal 6 ist 12.

"Das ist dreimal 6." -> dreimal 6 ist 18
Ab hier kann das Kind alleine weitermachen. Die Kontrolle kann stets mit der Kontrolltafel 1 erfolgen.
Liegen zehn 6er-Stäbchen sowie sechs 10er-Stäbchen erkennt das Kind die gleiche Menge der Perlen.
Analyse der Multiplikation - Multiplizieren mit 10
Wieder bitte ich das Kind, mir eine Zahl zu nennen. (Am Beispiel nehme ich wieder die 6.) Auf einen kleinen Zettel schreibe ich • 10 und lege diesen neben das 6er-Stäbchen. "Das 6er-Stäbchen soll zehnmal gelegt werden" -> Kind legt zehn 6er-Stäbchen untereinander.
"Wie viel ist zehnmal 6?" -> 60. "Kannst du das in 10er-Stäbchen legen?" -> Kind legt sechs 10er-Stäbchen unter die farbigen 6er-Stäbchen. "Wie viele 10er-Stäbchen liegen dort?" -> 6. Ich schreibe die 6 auf einen weiteren kleinen Zettle und lege diesen unter die 10er-Stäbchen.

Ich schneide die Null von der obenliegenden 10 ab und lege sie unten neben die Sechs. "Zehnmal muss ich nicht rechnen! Ich nehme die Null von der 10 und hänge sie an die Sechs ran."
Übungen
So können alle Multiplikationen des kleinen Einmaleins mit der 10 auf den Arbeitsteppich nebeneinander gelegt werden. Hier kann das Kind alleine weiterarbeiten.
Vergleichen gleicher Produkte
Ich lege mit den goldenen Perlen ein beliebiges Produkt, zum Beispiel 18. "Aus welchen gleichen farbigen Stäbchen können wir noch 18 bilden?" Das Kind legt alle Optionen, die 18 ergeben. Ggf. legt es auch 18 rote 1er-Perlen. Ich sage, dass 18 mal eine Zahl nicht mehr zu den Grundaufgaben gehört. "Die Zahl, die ich malnehme, muss kleiner als 10 sein."
Das Kind legt die Optionen 9 • 2, 6 • 3, 2 • 9 und 3 • 6. Ich lege 9 • 2 und 2 • 9 untereinander und sage: "9 • 2 ist das gleiche wie 2 • 9. Das nennen wir Tauschaufgaben. Tauschaufgaben haben immer das gleiche Ergebnis. Siehst du noch eine Tauschaufgabe?" -> 6 • 3 ist das gleiche wie 3 • 6.
Übungen
Auslegen aller möglichen Kombinationen der Produkte der Grundaufgaben. Entweder hat man hier vorbereitete Kärtchen, auf denen oben das Produkt steht und darunter Raum für alle Möglichkeiten der Perlenkombinationen oder man stellt sich eine lange Rolle her mit allen Produkten der Grundaufgaben. Hier kann das Kind dann ALLE möglichen Kombinationen auslegen.
Auch können ähnliche Reihen untersucht werden, wie die 3er / 6er und 9er Reihe, die 2er / 4er / und 8er Reihe oder die 5er und 10er Reihe.
Ich bitte das Kind, immer so viele Stäbchen zu legen, wie das farbige Stäbchen Perlen hat. Das Kind bildet so alle Quadratzahlen.
Einführung
"Nenne mir eine Zahl zwischen 3 und 9." -> 4 Ich nehme das weiße 4er-Plättchen und schiebe es von links in das Brett. Das rote runde Plättchen setze ich auf die 1. "1 mal 4." Ich nehme vier rote Perlen und lege sie zählend von oben nach unten in die erste Reihe "1, 2, 3, 4. 1 mal 4 ist gleich 4. Das können wir in das Heftchen übertragen." Ich schreibe in das Aufgabenheftchen 1 • 4 = 4. Das Kind führt die 4er-Reihe fort bis 10 • 4.
Das kleine Einmaleins ist nicht Voraussetzung. Das Kind rechnet additiv oder auch zählend. Die Ergebnisse werden immer sofort eingeschrieben!
Die Kontrolle erfolgt mit der Kontrolltafel 1 (alle Lösungen enthalten). Nun kann das Kind die übrigen Reihen legen, zählen und das Ergebnis notieren. Auch hier erfolgt die Kontrolle über die erste Tabelle.
Übungen:
Im Anschluss an das Legen aller Reihen des Einmaleins kann das Kind nun mit dem Aufgabenkasten (gemischte Aufgaben des kleinen Einmaleins) arbeiten. Auch hier erfolgt die Kontrolle über die Kontrolltafel 1.
Es gibt drei Multiplikationstabellen und zwei Kontrolltafeln, da in der Multiplikation wie bei der Addition Tauschaufgaben gebildet werden können. Daher gibt es auch hier eine "halbe" Multiplikationstabelle sowie eine "halbe" Kontrolltafel mit den einfachen Multiplikationsaufgaben (größerer Faktor zuerst).
Tabelle 1
Das Kind zieht zum Beispiel 3 • 4 aus der Box mit den Grundaufgaben. Der rechte Zeigefinger geht auf die blaue 3, der linke
auf die rote 4. Beide Finger bewegen sich senkrecht bzw. horizontal aufeinander zu. Das Ergebnis liegt dort, wo die beiden Zeigefinger sich treffen. Die Aufgaben können aufgeschrieben
werden.
Tabelle 2
Das Kind zieht zum Beispiel 4 • 3 aus der Box mit den Grundaufgaben. Der rechte Zeigefinger geht auf den kleineren Faktor, hier
die rote 3, und der linke Zeigefinger geht auf den größeren Faktor, die rote 4. Nun zieht das Kind den Zeigefinger der rechten Hand horizontal bis an das Ende der Reihe und dann senkrecht
nach unten, bis es die Reihe des linken Zeigefingers trifft. Nun bewegt sich der linke Zeigefinger horizontal nach rechts, bis die beiden Finger sich, hier auf der 12, treffen.
Tabelle 3
Das Kind sichert seine Kenntnisse im Bereich der Grundaufgaben der Multiplikation, indem es Aufgabenkärtchen zieht und das Ergebnis mit den Ergebnisplättchen aus der kleinen gelben Box auf die leere Tabelle legt. Fehlerkontrolle: Alle Plättchen können gelegt werden. / Kontrolltafeln
Ziele
Sichern der Grundaufgaben des kleinen Einsdurcheins / Zusammenhang zur Multiplikation erkennen
Verteilen von Perlenmengen bei gleichen Dividenden

Ich bitte das Kind (z.B.) 21 grüne Perlen in ein separates Schälchen zu zählen. "Diese 21 Perlen wollen wir jetzt gerecht auf 9 verteilen." Ich beginne die Püppchen auf das Brett zu stellen. Das Kind fährt fort. "Kannst du die Perlen an die Püppchen verteilen, so dass jedes gleich viel bekommt?" Das Kind verteilt die Perlen. Es bleiben 3 übrig.
"Die können wir nicht verteilen, die Perlen bleiben übrig. Das Ergebnis ist das ...?"-> was einer bekommt. "Das schreiben wir auf!"

"Wie viel haben wir verteilt?" -> 21. Ich schreibe 21 in die linke Spalte. "Auf wie viele haben wir verteilt?" -> 9. Ich zeige auf die 9. "Wie viel bekommt jeder einzelne?" -> 2. Ich schreibe 2 in die dritte Spalte. "Und wie viele bleiben im Schälchen übrig und können nicht verteilt werden?" -> 3. "Gut, das nennen wir auch den Rest."
Ich bitte das Kind die Perlen wieder zurück in das Schälchen zu legen und nehme ein Püppchen weg. "Jetzt verteilen wir die 21 Perlen auf acht Püppchen." Das Kind fährt fort.

Das Kind verteilt die Perlen so lange, bis die 9 Mulden des Bretts unter dem Divisor voll sind. "Wenn wir dem Püppchen keine Perlen mehr geben können, weil es keine freie Mulde mehr hat, müssen wir mit dem Verteilen der grünen Perlen aufhören."
Ich weise das Kind darauf hin, dass die Divisionen ohne Rest besonders wichtig sind und deshalb farbig hervorgehoben werden.
So können alle Dividenden bis 81 vom Kind auf ihre Teilbarkeit hin überprüft werden. Die gesammelten aufgeschriebenen Ergebnisse können zu einem eigenen Heftchen gebündelt werden.
Übung - Notieren aller Divisionen ohne Rest
Ähnlich wie eine Zahlenrolle kann das Kind nun alle Divisionen ohne Rest (farbig hervorgehoben) untereinander notieren. So stellt es seine eigene Rolle aller Grundaufgaben des kleinen Einsdurcheins her.
Übung - Grundaufgaben geordnet nach Divisor notieren
Entweder notiert das Kind aus seinen eigenen Notizen der vorangegangenen Arbeiten die Aufgaben geordnet oder es füllt ein Grundaufgabenheft aus.
Übung - Arbeit an der Kartei
Im Anschluss kann das Kind gemischte Aufgaben zur kleinen Division bearbeiten (Kontrolle rückseitig bzw. über die Kontrolltafel).
Der Einsatz der Tabellen und Kontrolltafeln erfolgt wie bei den bereits eingeführten Tabellen / Tafeln. Das Kind zieht eine Aufgabe aus der Box mit den Grundaufgaben, der rechte Zeigefinger geht auf den Dividenden (blaues Feld) und der linke Zeigefinger auf den Divisor. Wieder geht der rechte Zeigefinger senkrecht nach unten und der linke Zeigefinger horizontal nach rechts. Dort wo sich die Finger treffen, liegt das Ergebnis.
Primzahlen
Mit der Tabelle 1 werden Primzahlen eingeführt (Zahlen sind durch sich selbst und durch 1 teilbar). Diese Zahlen sind auf der blauen Reihe der Dividenden weiß!
Gleiches Ergebnis
Das Kind sortiert die Ergebnisplättchen aus der kleinen Box und "stapelt" gleiche Quotienten. Mithilfe der Tabelle 1 werden zu diesen Quotienten nun die Aufgaben ermittelt und die Plättchen werden dann in die entsprechenden leeren Felder der Tabelle 2 gelegt.













































